fanbion.blogg.se - Condense logarithms expression

#Condense logarithms expression how to#

\log_a (b) - \log_a (c) = \log_a (b \div c) A number times log expression Subtraction of two logs with the same base is done by dividing their exponents: \log_a (b) + \log_a (c) = \log_a (b \times c) Subtracting logarithms If we have two logs with the same base and we want to add them – multiply their exponents:

The calculator will use the entered variables and give you the result, which is: 5.67.

Enter the variables (x – given value of a number, n – given base, a – given exponent).

Let’s use the calculator and calculate the number times log equation: In addition, you can either add or find the difference of logarithms and calculate “number times log” expressions. Our calculator supports all three formulas we mentioned in the previous parts. Therefore, instead, you can use our condense logarithms calculator to simplify and calculate the log. The idea is that you are given a bunch of log expressions as sums and/or differences and your task is to put them back or compress into a nice one log expression. We showed you the formulas, but wait! Solving the logarithmic expressions all by yourself can be tedious and time-consuming. The reverse process of expanding logarithms is called combining or condensing logarithmic expressions into a single quantity. Simply, we do not explicitly write it.įor example: \log(100) – we can also write as \log_) = \log_2 (256 \div 16) = 16 Example: using the condense logarithms calculator Sometimes, if you see a logarithmic expression without a base, it means that the base is 10. Use the quotient and product rules to compress the three groups of expression, as shown below. Let’s begin by applying the power rule in the first term. Solution Let’s go ahead and condense the expressions inside the bracket first.

and answer (how many times we need to multiply the base to get the argument) Condense the logarithmic expression 1 3 3 log ( x + 4) + log ( x 1) log ( x 2 1) into a single logarithm.

base (a number that we multiply by the answer number).

Logarithmic expressions does not have only one log property, but three specific properties you should know:

So, the log is 3, and we write it down this way: \log_3 (27) = 3 For example, let’s look at the example below:ģ \times 3 \times 3 = 27 -> We need to multiply the number of 3 three times by itself to get 27. In algebra, you learn about logarithmic functions. However, everybody hears about this math concept in high school (algebra), if not even earlier. Thus, if you want to have basic math skills, you should definitely know them. In terms of math problems, logs are very useful in solving them. What is a logarithm?Ī logarithm is a math expression that tells us which power we need to raise a particular number, “a” to get a number “b”. Then, our calculator will solve the equation according to the formula you choose.Ĭheck out this math category if you need more math-related calculators besides this calculator. If you have any comments, questions, or suggestions, please contact Dr. With this useful tool, just enter log properties: the base and exponent. You can create an account and/or log in using the User menu in the top-right corner.

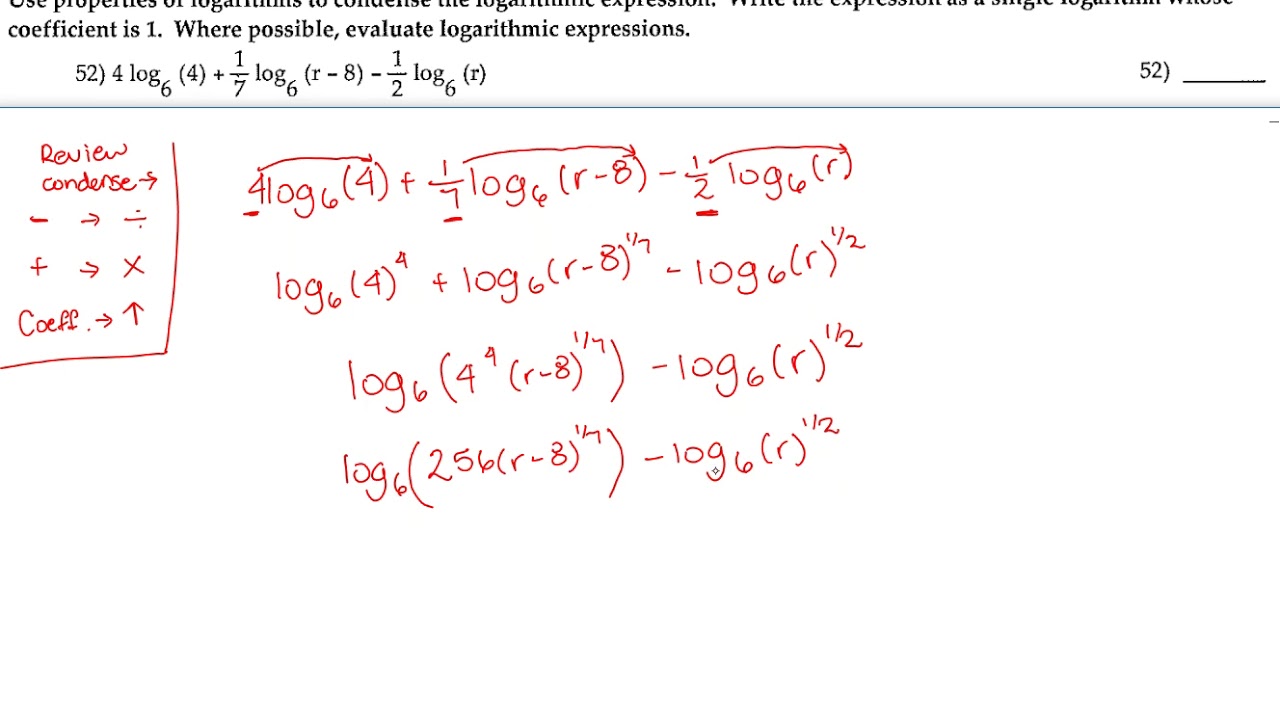
Solving a logarithmic equation with one log. Expanding and condensing log expressions (log distribution rules). Besides other online calculators, our Condense Logarithms Calculator provides a simple way to add, subtract and raise logs to a particular exponent. Evaluating simple logarithmic expressions.

#Condense logarithms expression how to#

We will learn later how to change the base of any logarithm before condensing.Condense Logarithms Calculator is a condensing logarithms step-by-step calculator. It is important to remember that the logarithms must have the same base to be combined. We can use the rules of logarithms we just learned to condense sums and differences with the same base as a single logarithm. In the following video, we show another example of expanding logarithms.